This picture shows an electric pole, there is no force because the two wires produce alternating currents, meaning that they will be continuously canceling each other.
We worked with the magnetic field at the center of a current loop lab, this lab consisted on measuring the magnetic field change due to a number of loops. First of all, we used a magnetic field sensor, and calibrated it in order to eliminate the effects of the Earth's magnetic field. Then we used copper wire to wrap a test tube to create the loops, and finally the magnetic field of each loop was calculated through logger pro.
This picture shows the magnetic field due to a certain amount of copper loops, as we can see, the magnitude of magnetic field is directly proportional to the number of loops, when the current and voltage are constant.
A galvanometer is an instrument that detects electric current. Professor Mason showed us that when a magnet is pull out and push in into a copper wire with many loops, it produces an induced electric current, and the faster it is pulled or pushed, the current increases.
These are factors that help maximize the current. Another important factor is the area between the magnet and the number of loops, if its smaller, current increases.
This experiment proves Faraday's law, Professor Mason added a coil that is insulated, the coil is placed above the previous coil, there is no direct electric contact; however, the alternating magnetic field induces an alternating current which lights up the bulb. If the coil is moved up, it gets dimmer. If the magnetic field is increased, even though the coil is not touching the metallic bar, if also lights up, since the magnetic field is going upwards, it is possible that it reaches the coil.
After this, Professor Mason added a copper coil, the magnetic field of this coil points in the opposite direction compared to the first coil. As the magnetic field going upwards increases, the copper coil starts to levitate.Then, Professor Mason added an aluminum coil, the silver coil levitated higher because the density was lower than the copper coil.
The next one was a steel ring with a gap in between, which means that current can't flow, so nothing will happen.
The next experiment is applied to Lenz's Law, Professor Mason dropped two magnets through two different tubes, one made of aluminum and another made of glass. We observed that the magnet running inside the glass landed way before the aluminum did because for the aluminum case there was a change in magnetic flux, as the magnet was sliding down it generated a current moving counterclockwise in the aluminum that slowed the magnet down since there was a magnetic field going up as a consequence. This was not a magnetic effect because Aluminum is not a magnetic material, however, aluminum is a conductor, so it was the current that effected the magnet.
Here we derived an expression for emf by using magnetic flux and magnetic field equations.
We then drew the graphs of magnetic field and emf as a function of time. The magnetic field has a sine function whereas the emf has a negative cosine function.



























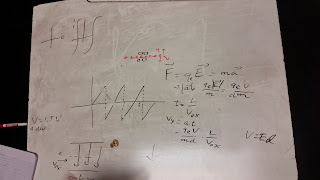

.jpg)

















